Paperproof ⚔️ Lean's #explode
This post compares Paperproof vscode extension with Mathlib's #explode command - how exactly does each display a proof; what was the motivation behind writing each tool; and what Lean objects they use internally.
Apart from the default Infoview, Lean has two proof visualisations:
- #explode command (by Mario Carneiro), and
- Paperproof (by Anton Kovsharov and Evgenia Karunus).
Let's see how both of these render the very same proof:
theorem hi (a b : Prop) : a ∧ b → b ∧ a := by
intro ab
cases' ab with hA hB
apply And.intro
exact hB
exact hA#explode
#explode is a command in Mathlib. You can use it by importing the relevant file with import Mathlib.Tactic.Explode, and writing #explode your-theorem-name.
See the example output below:
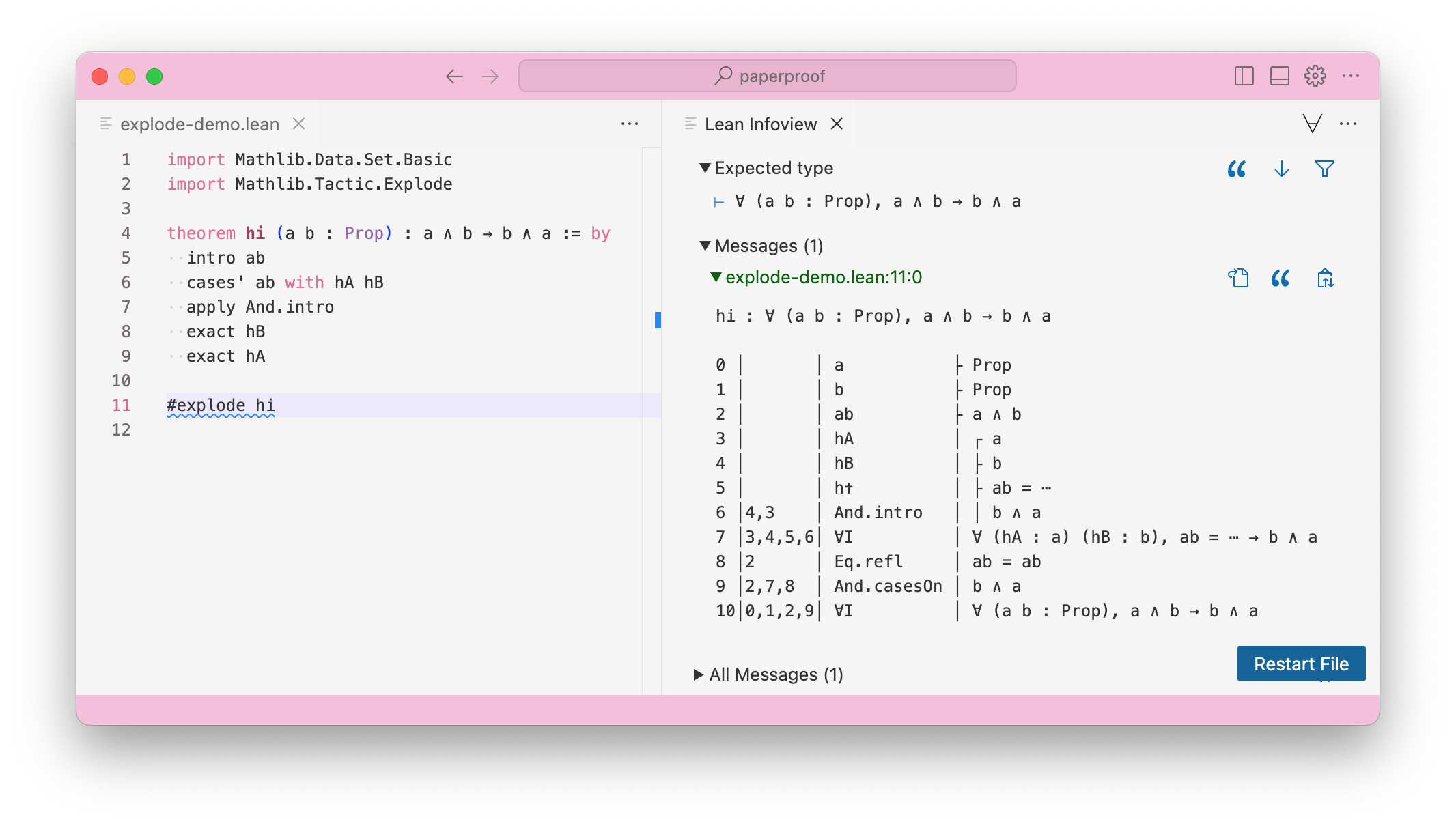
#explodePaperproof
Paperproof is a vscode extension. This is how you would use Paperproof to render the same proof:
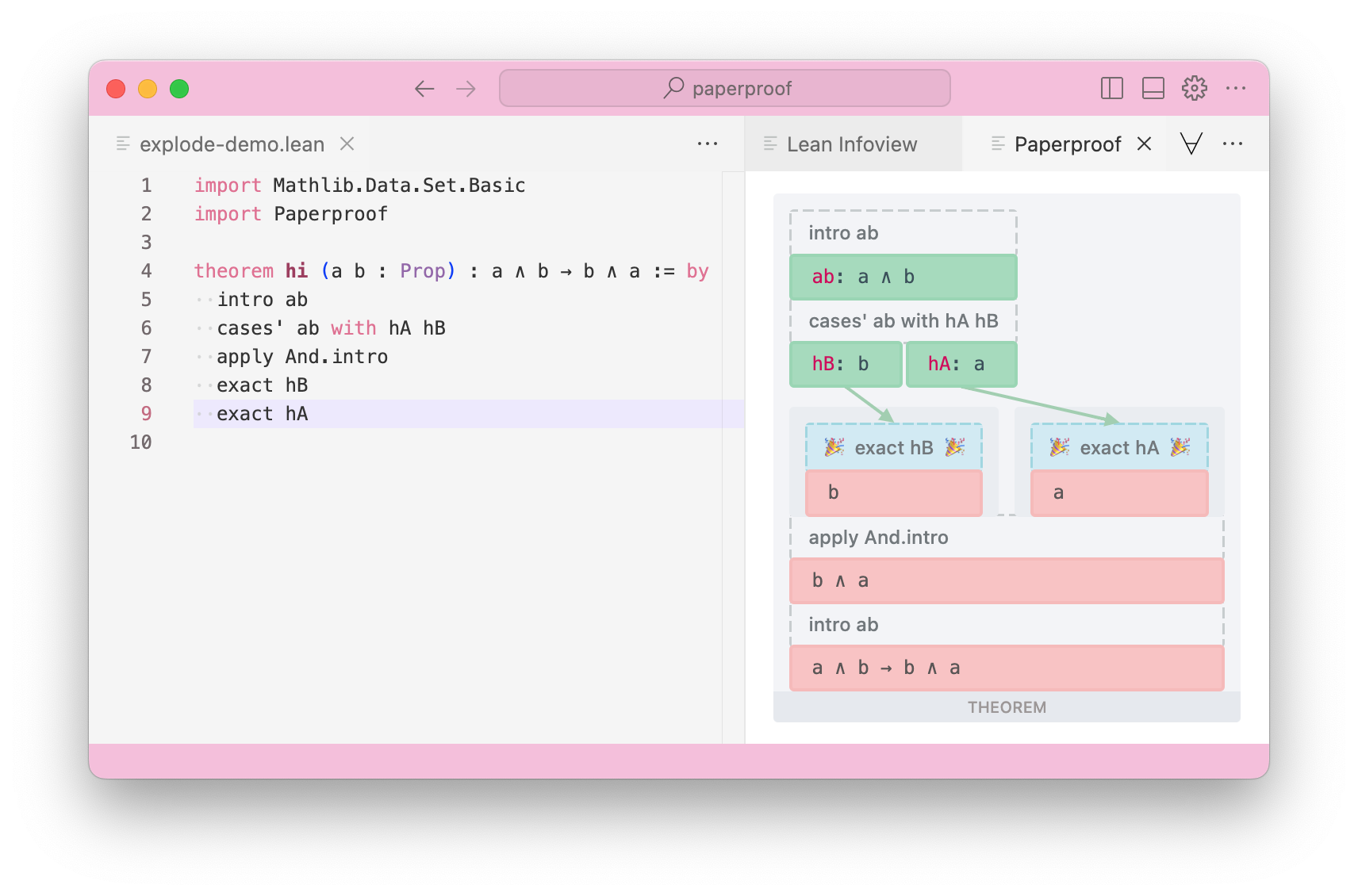
Comparison
To anyone who has skimmed through a beginner logic textbook, the main difference will be apparent - #explode visualises Lean proofs as a Fitch Table, and Paperproof visualises Lean proofs as a Gentzen Tree.
What's less obvious is the fact that they use two different data structures to glean information from a Lean proof.
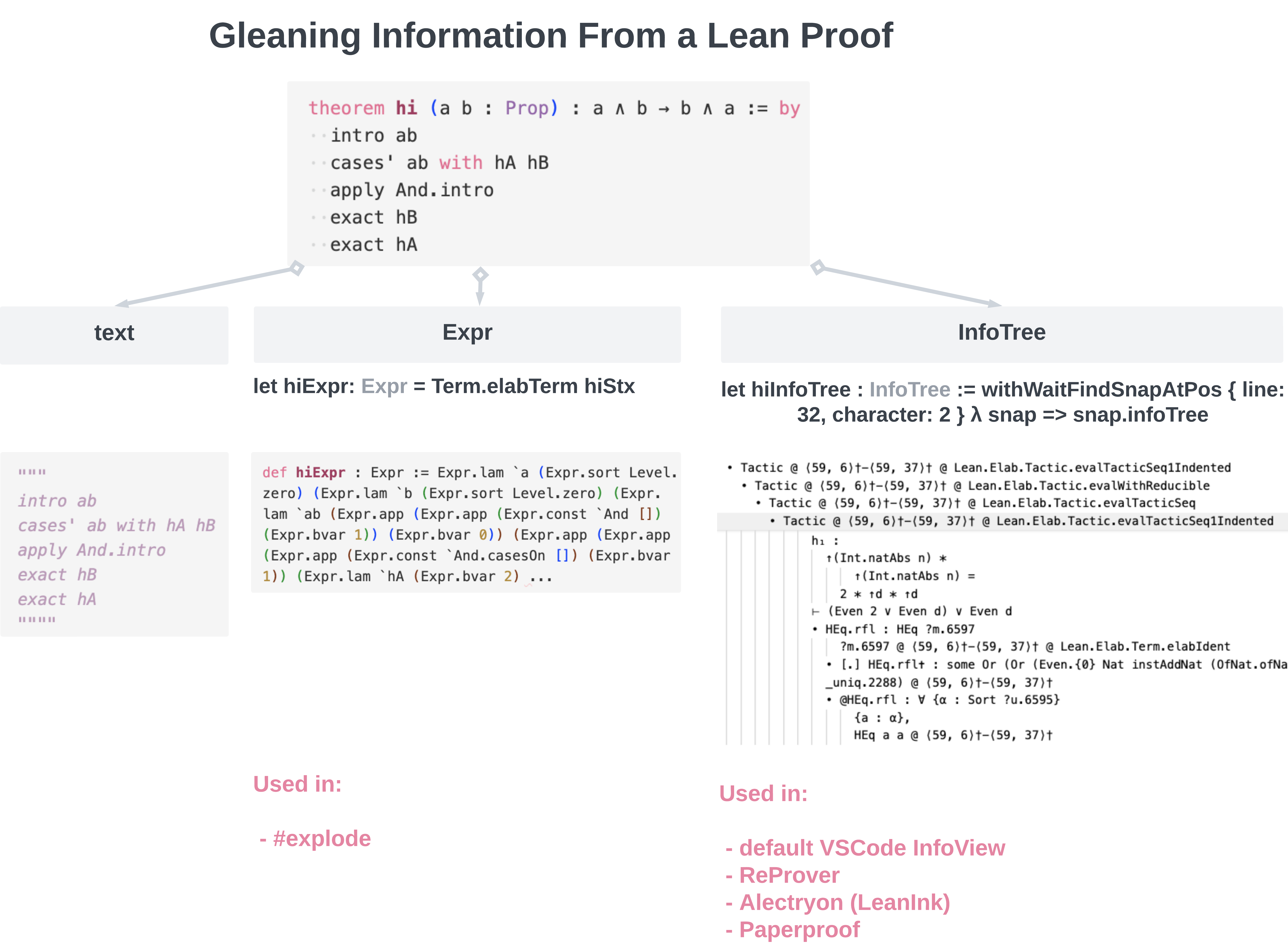
For any given proof statement, we have 3 options:
- text - simply parse the
.leanfile as a text file. This will give us a string of tactics.
This is a silly option of course - the real code in Lean is the types that get created by applying tactics, not the tactics themselves!
But I find that giving this option for completenes makes it easier to understand what the other two options are doing, fundamentally. Expr- this will render your proof in terms of lambda abstractions and applications. You will get output similar to what you get when you use the#printcommand.
Notice that this loses you a lot of information - you do not know what exact tactics were applied, you only know the resulting proof term. For all you know, there are infinitely many ways to construct the very same proof term.-
InfoTree- this gives you a sequence of tactics that were applied in a proof. Per each tactic, you get two lists: "a list of goals and their hypotheses" before this tactic was applied, and "a list of goals and their hypotheses" after this tactic was applied.
[conspiracy theory]
Hey, might it be that the "Infoview" title comes from "InfoTree" (Lean data structure that's used to glean information from the Lean proof) + "Webview" (vscode's name for the vscode panel where the Infoview and other such interfaces can be rendered).
These options and their corresponding output can be seen in the diagram below.
To drive the point home on how tragic it is to lose all tactic information, let's create our own tactic:
elab "ourOwnTactic" : tactic => do
let mvarId ← getMainGoal
let term ← `(λ a b ab => And.casesOn (motive := λ t => ab = t → b ∧ a) ab (λ hA hB _ => And.intro hB hA) (Eq.refl ab))
let expr ← elabTerm term none
mvarId.assign exprAs you see, our tactic simply assigns the entire proofterm to the theorem in one sweep.
| tactic proof | proofterm proof | ourOwnTactic proof |
|---|---|---|
| | |
Three different ways to prove the same theorem that result in the very same Expr. | ||
So, despite the fact that vastly different code was used to prove the hi theorem, our Expr stays the same, and the visualisation that's based on Exprs will render all three proofs above in exactly the same way.
Now, back to the difference between #explode and Paperproof - how do each of these glean information from the Lean proof?
#explode uses Exprs, and Paperproof uses InfoTrees. The only reason you seem to see a reasonably high-level proofs in #explode is because many Lean tactics are low-level already (intro is just lambda abstraction, apply is just lambda application).
Let's summarise the situation in a table below:
| low-level ( Expr) | high-level ( InfoTree) | |
|---|---|---|
| table |  | ??? |
| tree | ??? | 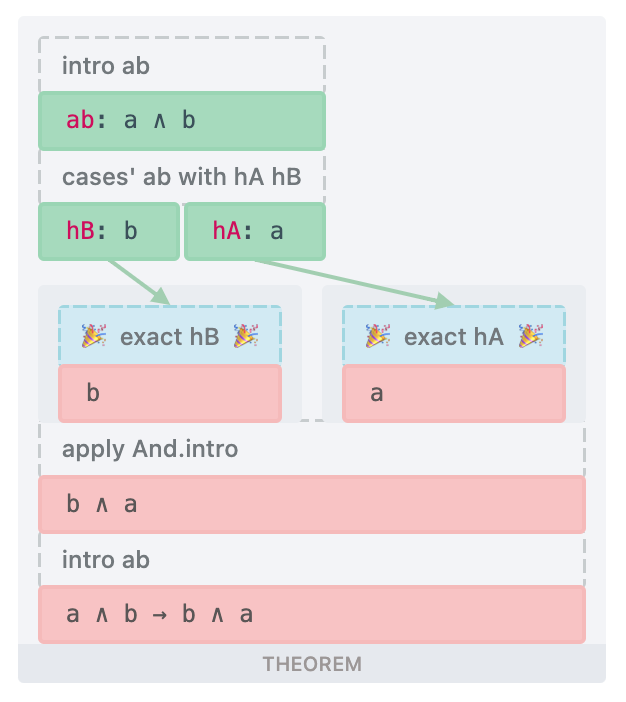 |
So, why does #explode use Exprs? Because there exists a way to translate low-level stuff (calculus of inductive constructions) into a Fitch Table interface, and there is no way to translate high-level stuff (tactics) into a Fitch Table interface? No, #explode could potentially display both Expr data and InfoTree data.
The same goes for Paperproof - Paperproof could well render both Expr data and InfoTree data.
Mario Carneiro went for Exprs because he specifically created #explode in order to get a glimpse into what proof term extremely high-level tactics such as simp result in. That's the entire purpose of the #explode command.
The reason why Paperproof uses InfoTrees is because, like described above, it would be really tragic to lose all the tactic information. We want to display exactly the abstraction level that the proof author intended. Paperproof specifically aims to be a one-to-one mapping of the proof written to the proof displayed.
[evgenia's biography]
In fact, Paperproof stumbled upon theExprvsInfoTreechoice early on. Before I understood I should useInfoTrees for the Paperproof's parser, I ported the #explode command from Lean 3 to Lean 4 (link), thinking that I might build a Paperproof tree by adjusting #explode's output.
In either case, we now have two missing cells - a Fitch Table that renders high-level details (#explode + InfoTree), and a Gentzen Tree that renders low-level details (Paperproof + Expr). Regarding the former, a PR into Mathlib might be welcome. The latter, Expr rendering in Paperproof, would certainly be a welcome addition to Paperproof. You can read more on that in "Can Paperproof render proof terms?".