Paperproof ♥️ Natural Deduction

In this post and the accompanying Paperproof ♥ Semantic Tableaux post, we will be using Lean's deductive apparatus (Calculus of Inductive Constructions) and its visualisation (Paperproof) as a metalanguage to implement proof trees from Natural Deduction and Semantic Tableaux. 

Why would we do this? The reason is twofold - as we'll see below, once we understand Lean's deductive apparatus, we will consider most other deductive apparata perfectly intuitive. For example, memorizing the inference rules for semantic tableaux gets reduced to memorizing the "we follow normal Lean logic, except we always start with by_contra ("prove by contradiction" tactic), and we are only allowed to do top-down proofs from now on" rule. Secondly, if you already know Natural Deduction or Semantic Tableaux deductive apparata, you should find Lean's deductive apparatus as seen in Paperproof easier to get used to - and explicitly drawing parallels, as we do in these posts, should help you.

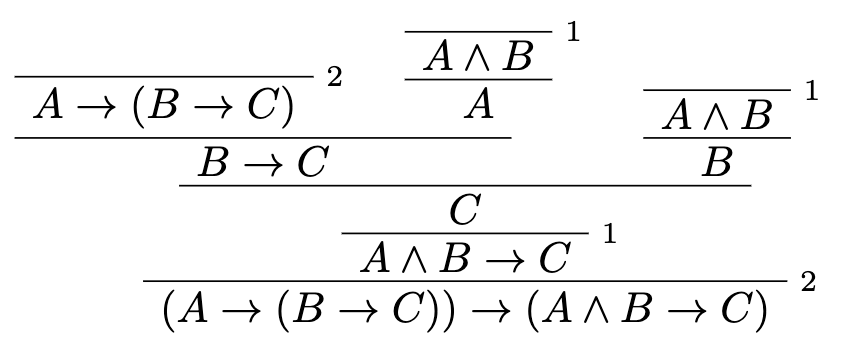
While semantic tableau (see Paperproof vs Semantic Tableaux) is a strictly top-down  mechanism,  with natural deduction we can employ both top-down and bottom-up reasoning to construct a proof.

Look at the natural deduction proof tree above. In Lean terms - which wff (well-formed formula) is a hypothesis here, and which wff is a goal?
We can say with certainty that the wffs at the very top (A → (B → C), A ∧ B, A ∧ B) are hypotheses, and the wff at the very bottom ((A → (B → C)) → (A ∧ B → C)) is a goal. Every wff in-between, however, can be considered either one or the other!

In natural deduction, we don't really care about the hypothesis/goal distinction, what we really want is to weave a pattern using our inference rules in a way that would lead us into an accepting state on top. Accepting state here is simply "the exact hypothesis we were given in the very beginning of the proof".

Below I'm listing basic building blocks of natural deduction.
I take these natural deduction rules from the "Logic and Proof" textbook (Jeremy Avigad, Robert Lewis, Floris van Doorn). As I mentioned, given a particular natural deduction tree, both the top-down and bottom-up interpretations of particular steps is a fine interpretation. Each of these basic building blocks can be applied either to a hypothesis (aka top-down proof), or to a goal (aka bottom-up proof). To hit the point home, I'll be showing both variants.

Basic building blocks
Natural Deduction	Lean
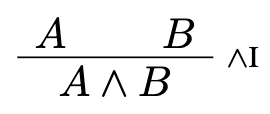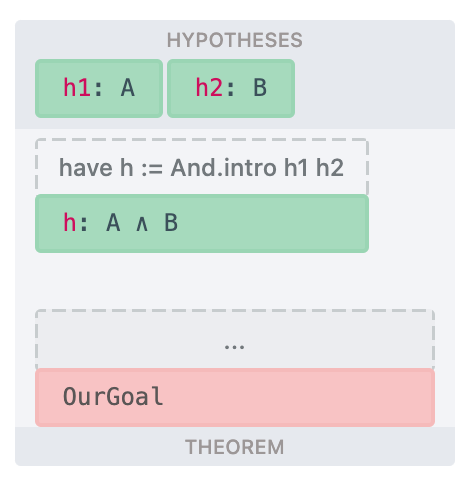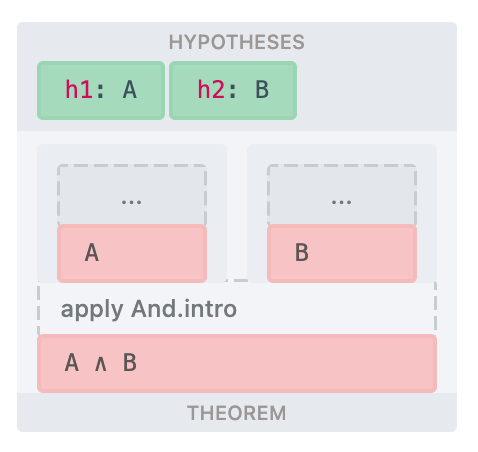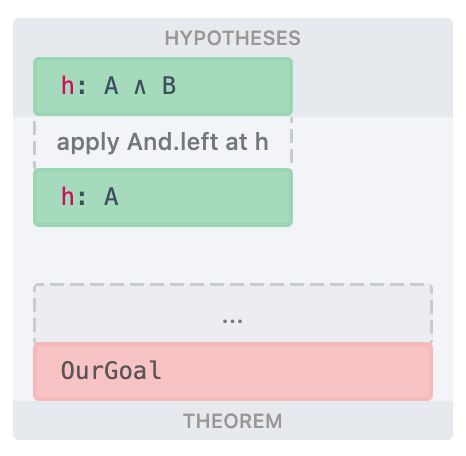I omit the remaining rules for conciseness - you can see all 10 rules (for both the propositional logic and predictate logic) in the following file github.com/Paper-Proof/paperproof/.../NaturalDeduction.lean.  The rules for the predicate logic are particularly interesting to explore.

Now, let's take a look at full-fledged proofs. The natural deduction proof tree is take, again, from the "Logic and Proof" textbook (Jeremy Avigad, Robert Lewis, Floris van Doorn).

Full proof of (A → (B → C)) → (A ∧ B → C)
Natural Deduction	Lean
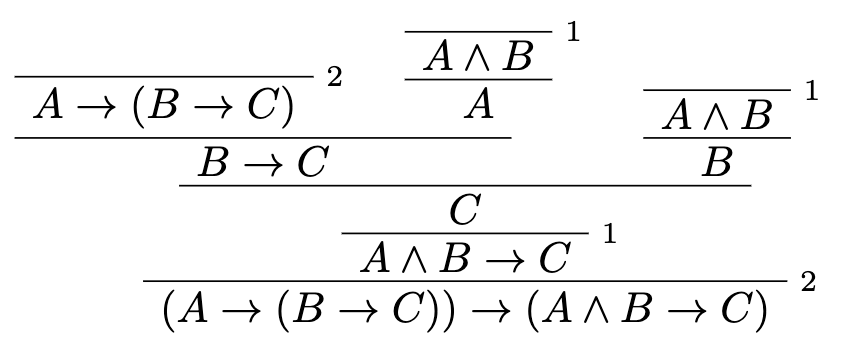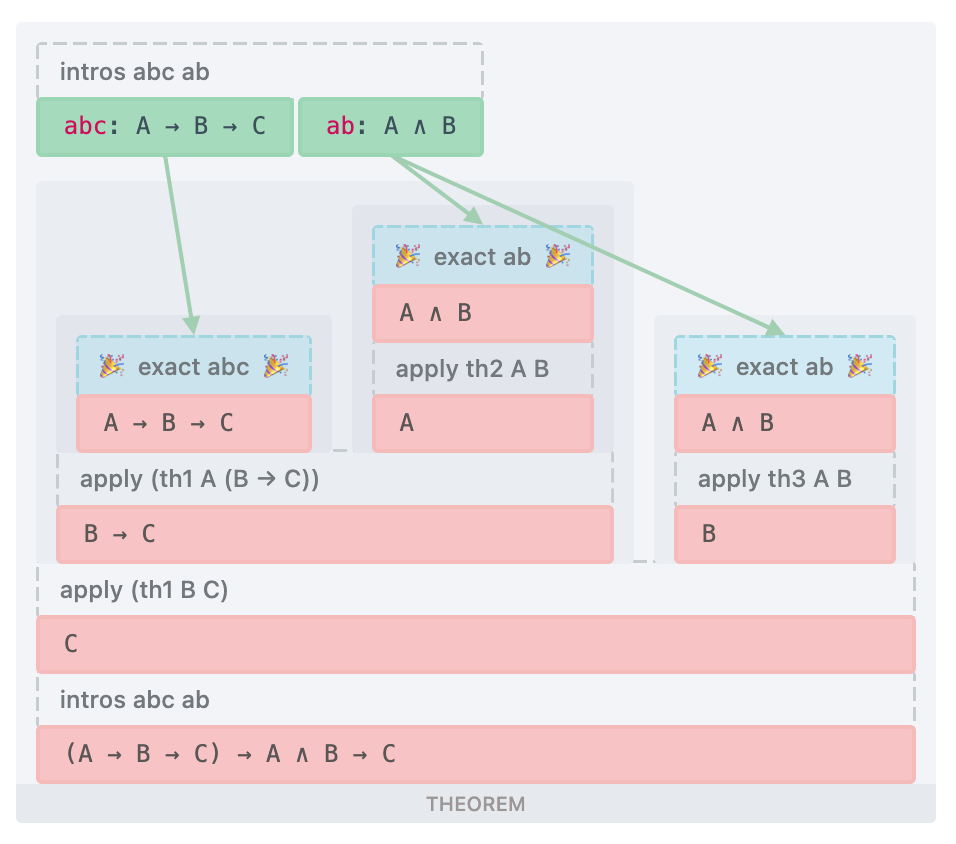