Paperproof ♥️ Semantic Tableaux

In this post and the accompanying Paperproof ♥ Natural Deduction post, we will be using Lean's deductive apparatus (Calculus of Inductive Constructions) and its visualisation (Paperproof) as a metalanguage to implement proof trees from Natural Deduction and Semantic Tableaux. 

Why would we do this? The reason is twofold - as we'll see below, once we understand Lean's deductive apparatus, we will consider most other deductive apparata perfectly intuitive. For example, memorizing the inference rules for semantic tableaux gets reduced to memorizing the "we follow normal Lean logic, except we always start with by_contra ("prove by contradiction" tactic), and we are only allowed to do top-down proofs from now on" rule. Secondly, if you already know Natural Deduction or Semantic Tableaux deductive apparata, you should find Lean's deductive apparatus as seen in Paperproof easier to get used to - and explicitly drawing parallels, as we do in these posts, should help you.

Instead of tableau formulations, it is more interesting sometimes to work with sequent systems; it is more or less obvious, in certain cases, that one can translate from one type of system to another: this is frequently quoted as "tableau systems are sequent systems upside down, and vice versa".

On sequents and tableaux for many-valued logics (Walter A. Carnielli, 1991)

Semantic Tableaux is what would happen if we started our every Lean proof by contradicting our goal, thus turning our proof into a strictly top-down proof. Meaning, to mimick Semantic Tableaux proofs in Lean, we want to:

• turn our goal (well, it's negation) *into a hypothesis*, and
• turn all further goals into Falses.

Usually lean proofs are a mix of bottom-up and top-down steps, but this lets us construct a fully top-down proof!

Here is a couple of basic buildings blocks for the semantic tableaux proofs. Both are taken form Smullyan's "A Beginner's Guide to Mathematical Logic".

Basic building blocks
Semantic tableau	Lean
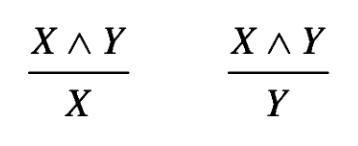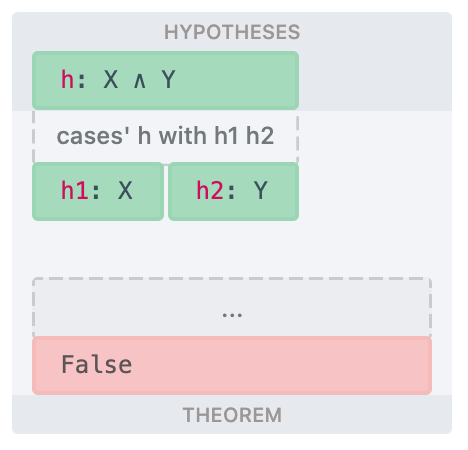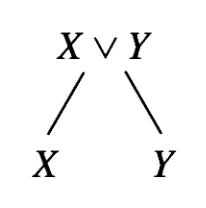
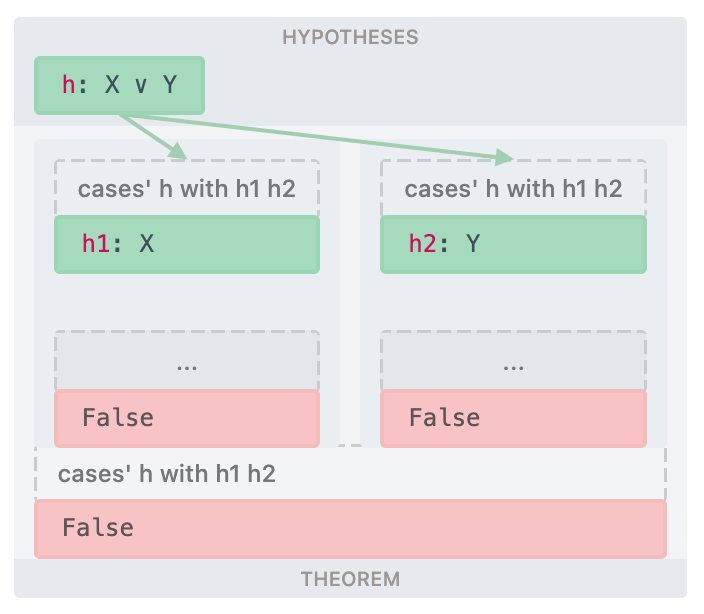I omit the remaining rules for conciseness - you can see all 11 rules (for both the propositional logic and predictate logic) in the following file github.com/Paper-Proof/paperproof/.../SemanticTableaux.lean.

Now, let's take a look at full-fledged proofs. All semantic tableau proof trees are taken from the excellent Tree Proof Generator by Wolfgang Schwarz (link).

Full proof of ((p ∨ q) ∧ (q → p)) → p
Semantic tableau	Lean
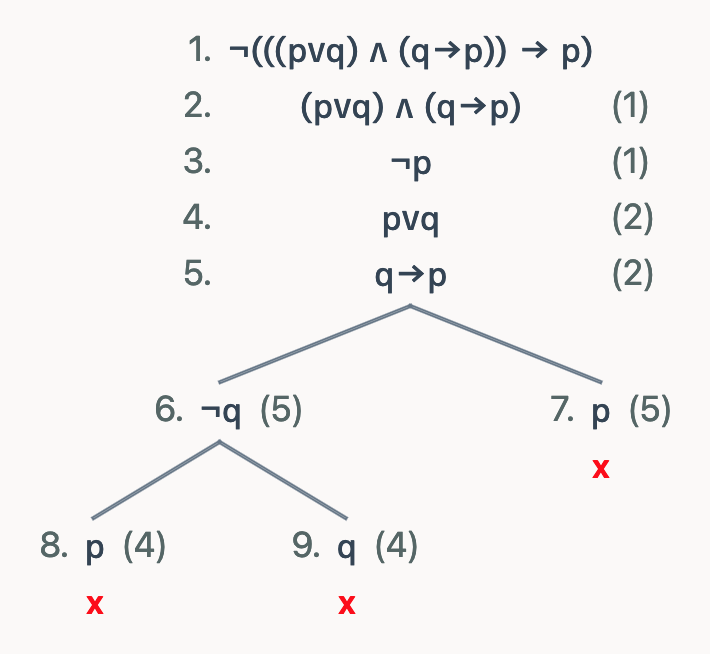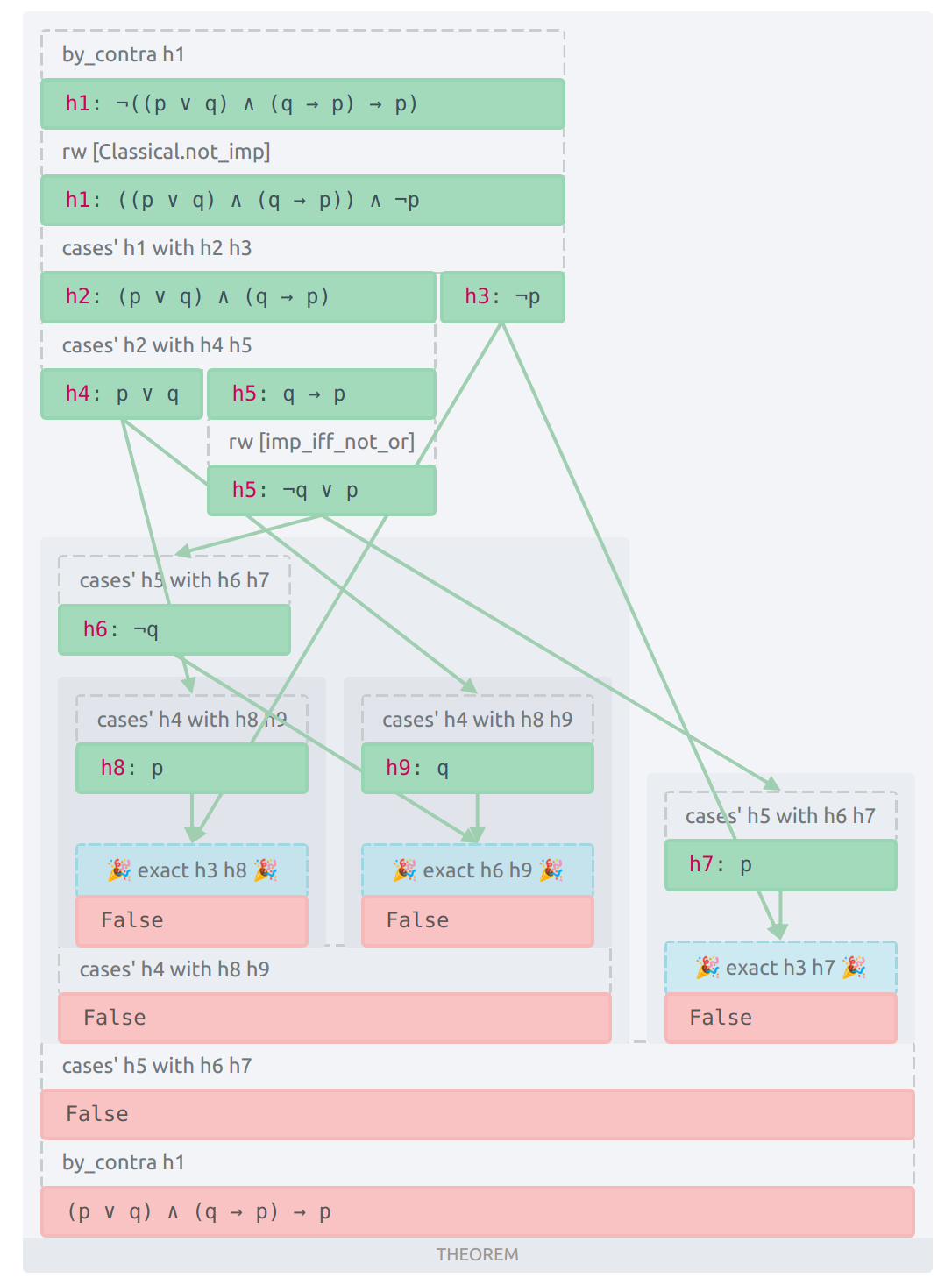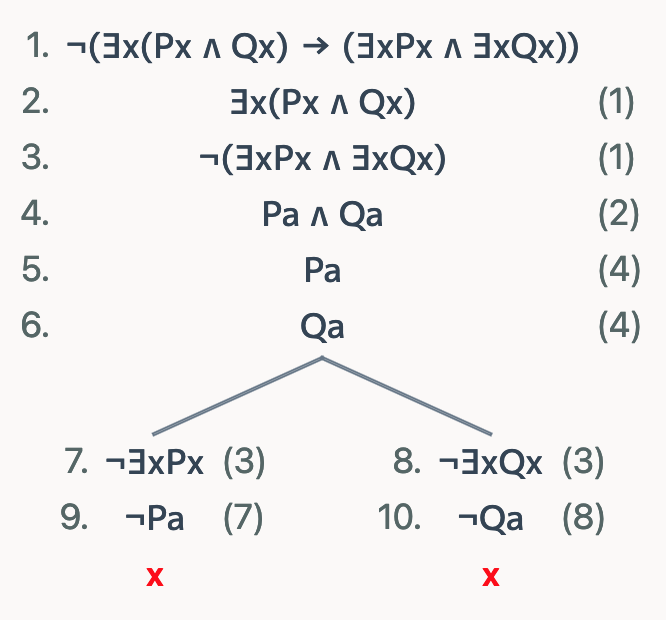
Full proof of ∃x(Px ∧ Qx) → ∃x(Px) ∧ ∃x(Qx)
Semantic tableau	Lean

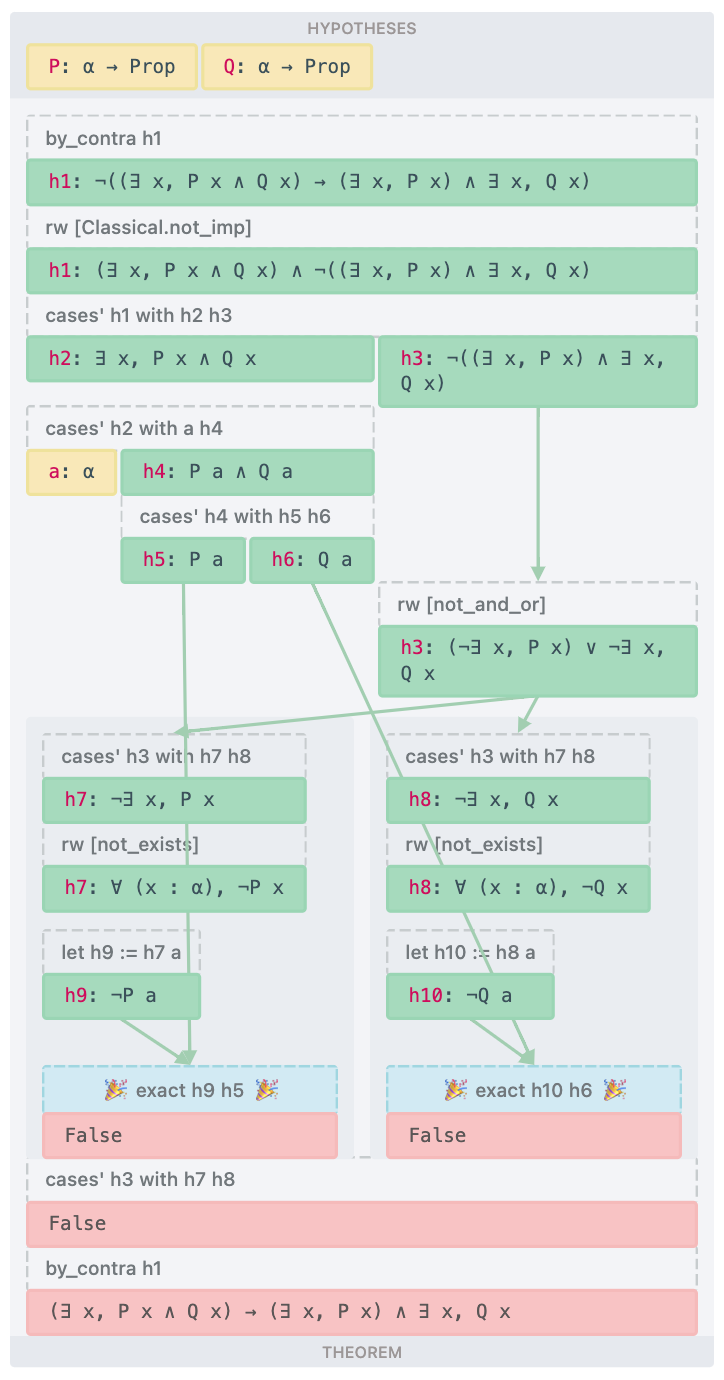So, semantic tableaux is what happens when we start the proof by contradiction in Lean. You can play with these rules yourself by opening a Paperproof online interface (https://codespaces.new/Paper-Proof/paperproof) and going to this file github.com/Paper-Proof/paperproof/.../SemanticTableaux.lean.