Paperproof's Architecture
This post is about the internals of Paperproof.
It's useful if you want to work on paperproof, on vscode-lean4, or if you want to create your own vscode extension for Lean/Coq/etc.
We have 3 pieces of code:
- extension codebase (code in /paperproof/extension)
Typescript code that you download when you install the Paperproof vscode extension. - webview codebase (code in /paperproof/app)
Typescript code. Technically a part of the extension codebase, but it's best to separate them in your mind. - Lean library codebase (code in /paperproof/lean).
This is Lean code that you import when you dorequire Paperproof from git "https://github.com/Paper-Proof/paperproof.git"@"main"/"lean"andimport Paperproof.
All of these pieces of code can talk to each other, and all of them possesses different information about what the user is up to.
What does each codebase know
Below you can see my vscode editor.
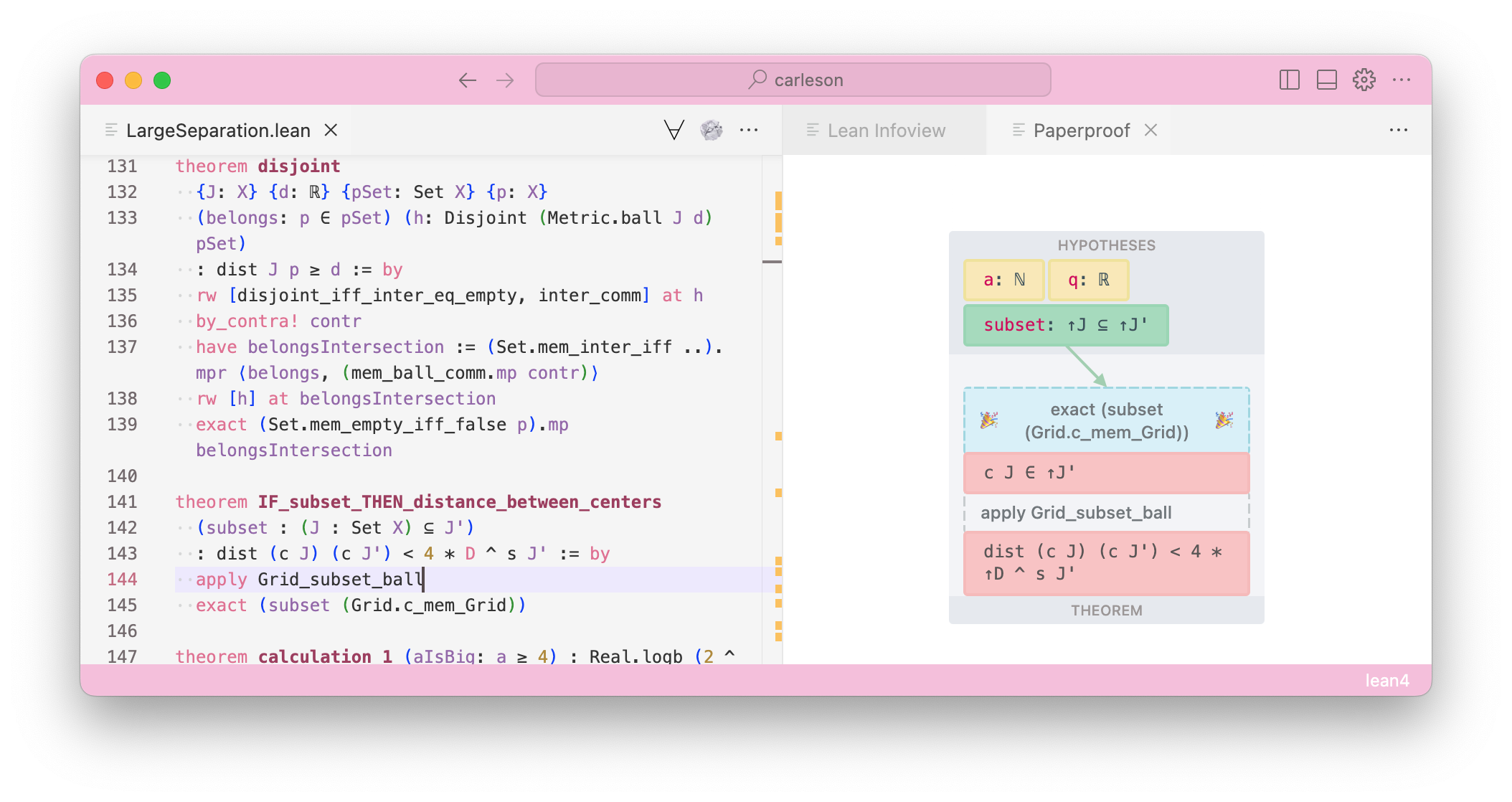
To be able to work on Paperproof (or, really, on any vscode exension), it's a good idea to get a sense for "what kind of knowledge is available to what codebase". Below I will list some examples:
- extension codebase
Knows everything the user is doing in the left panel (where your actual Lean theorems are).
For example, you can get a plaintext of this file; you can get a file name; you can determine when the user clicked on some line and character; you can determine what text the user just selected; you can subscribe to the "user typed something" event. - webview codebase
Controls everything in the panel on the right.
Unlike the extension, webview will know when the user clicked on some green hypothesis rectangle. Consider this a normal webpage - you can determine if the user typed something within your <input/> field in the webview, you can determine if the user pressed some shortcut, you can send the ajax request. Anything a browser can do, a webview can do. - Lean library codebase
Even though extension codebase technically knows everything that's going on in your project (it can copy the contents of any file in your workspace!), it can only work with plaintext files. On the left of my editor, you can see Lean code - and extension on its own only sees it as, well, text. However, we frequently want to understand the structure of this code in a deeper manner.
For example, I might want to determine if this Lean-looking plaintext even compiles.
I might want to determine what goals and hypotheses were available at line 137 character 20.
I might want to glean the entire history of this theorem by parsing this theorem's InfoTree.
This is the kind of information that Lean compiler (an entity that's really good at converting plaintext into Lean, remember) knows, and we can ask Lean library about these things.
How these codebases talk to each other
So - extension, webview, and Lean library have access to different information, and we need some way to share this information between these codebases to make Paperproof work.
For example, every time the user clicks on a tactic within some theorem, we want to detect line and character of that mouse click (extension knows that); detect the InfoTree that belongs to that line and character (Lean library knows that); and display that InfoTree as a Paperproof tree in the webview (Webview can do that).
There are exactly three types of communication between these codebases:
- extension talks to webview via
.postMessage()calls - webview talks to extension via
.postMessage()calls - extension talks to Lean library via RPC calls
Extension → Webview; Webview → Extension
As just said, both of these communications happen via .postMessage() calls.
.postMessage() is a normal, widely supported browser api - it works in vscode (reminder that vscode is a browser-based editor, at the moment of writing it uses Chrome v128), and it will work in all modern browsers. Although widely supported, this api is rarely used in web development - working on a vscode extension was the first time I had to deal with it.
.postMessage() was developed to enable communication between a document and the iframe embedded in it. To quote the docs:
The Channel Messaging API allows two separate scripts running in different browsing contexts attached to the same document (e.g., two
<iframe>elements, the main document and a single<iframe>) to communicate directly, passing messages between each other through two-way channels (or pipes) with a port at each end.
(From developer.mozilla.org/en-US/docs/Web/API/Channel_Messaging_API/Using_channel_messaging)
As it stands, "webview" in a vscode editor is nothing more than an <iframe> embedded in a particular space in vscode's html, as you can see in the screenshot below.
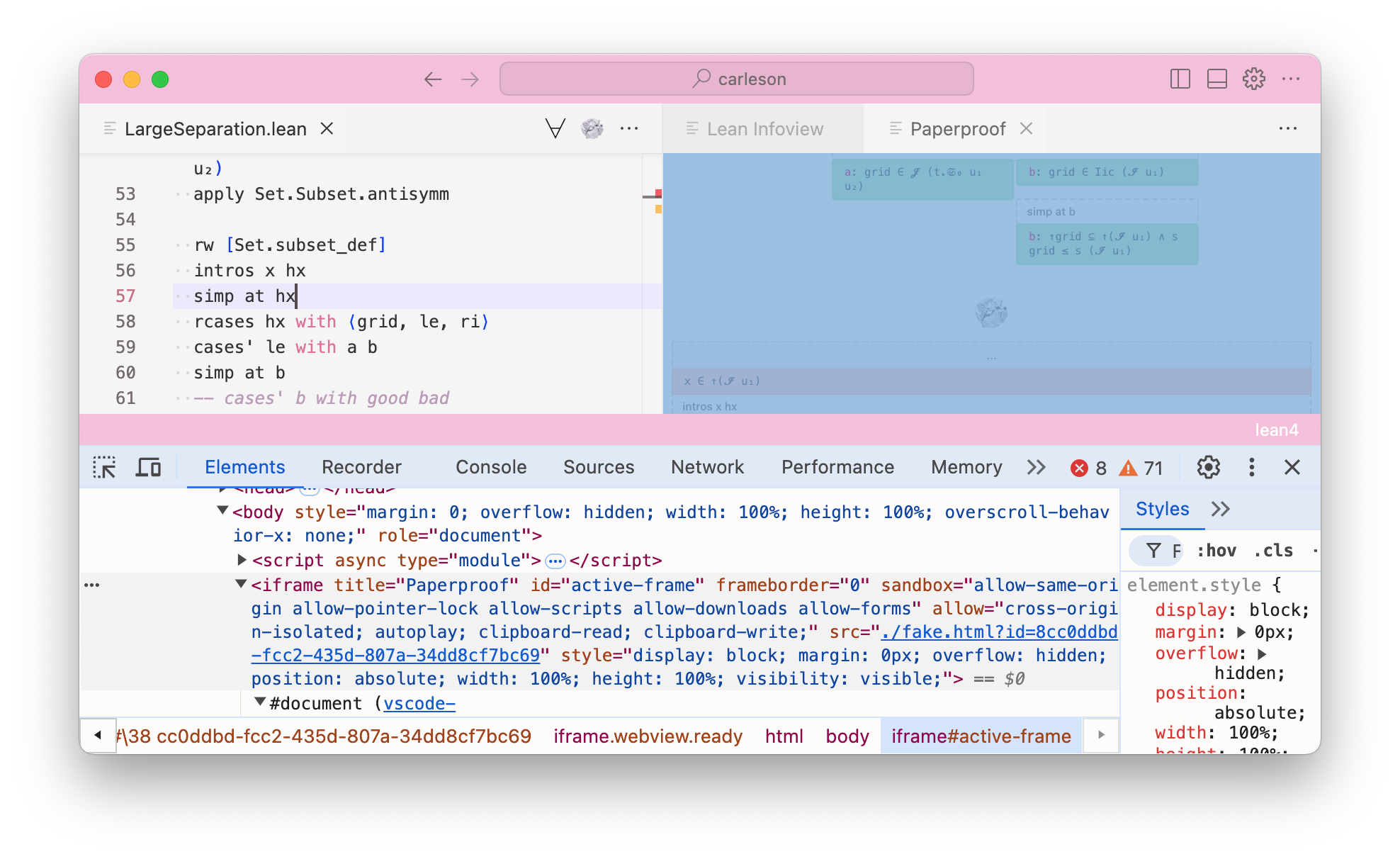
<iframe>.Hint:
CMD+SHIFT+P + "> Developer: Open Webview Developer Tools" command will open the dev console for you.So the conversation between our webview (embedded <iframe>) and extension (main document) happens via the .postMessage() calls as follows.
In webview:
const extension = acquireVsCodeApi();
extension.postMessage('hi hello');
addEventListener('message', (event) => {
const messageFromExtension = event.data;
...
});In extension:
const webview = vscode.window.createWebviewPanel(...);
webview.webview.postMessage('red blue green');
webview.webview.onDidReceiveMessage(async (message) => {
const messageFromWebview = message;
...
}Extension → Lean Library
Webview cannot directly talk to our Lean library, any such communicatin must happen with extension as an intermediary. Communication between the extension and Lean library happens via "RPC calls".
In extension:
const connection = await leanClient.sendRequest("$/lean/rpc/connect", { uri: editor.document.uri.toString() });
const response = await leanClient.sendRequest("$/lean/rpc/call", {
sessionId: connection.sessionId,
method: 'getOurInfoTree'
})In Lean library:
@[server_rpc_method]
def getOurInfoTree (params : InputParams) : RequestM (RequestTask OutputParams) := do
withWaitFindSnapAtPos params.pos fun snap => do
let parsedTree ← BetterParser snap.infoTree
...We get leanClient from the vscode-lean4 extension (default Lean interface that gives you the InfoView).
This setup is generally all you need to know, but if you'd like to get a good understanding of the internals of RPC requests, you can start by reading the vscode's official guide on Language Servers: link; and the corresponding Language Server implementation in Lean: link.
Lean objects of interest
Two most important Lean objects for Paperproof (and for Lean-Vscode) are Snapshot and InfoTree.
In Lean, each command (command is a syntax category - e.g., theorem is a command, lemma is a command, #lint is a command) is associated with a Snapshot Lean object.
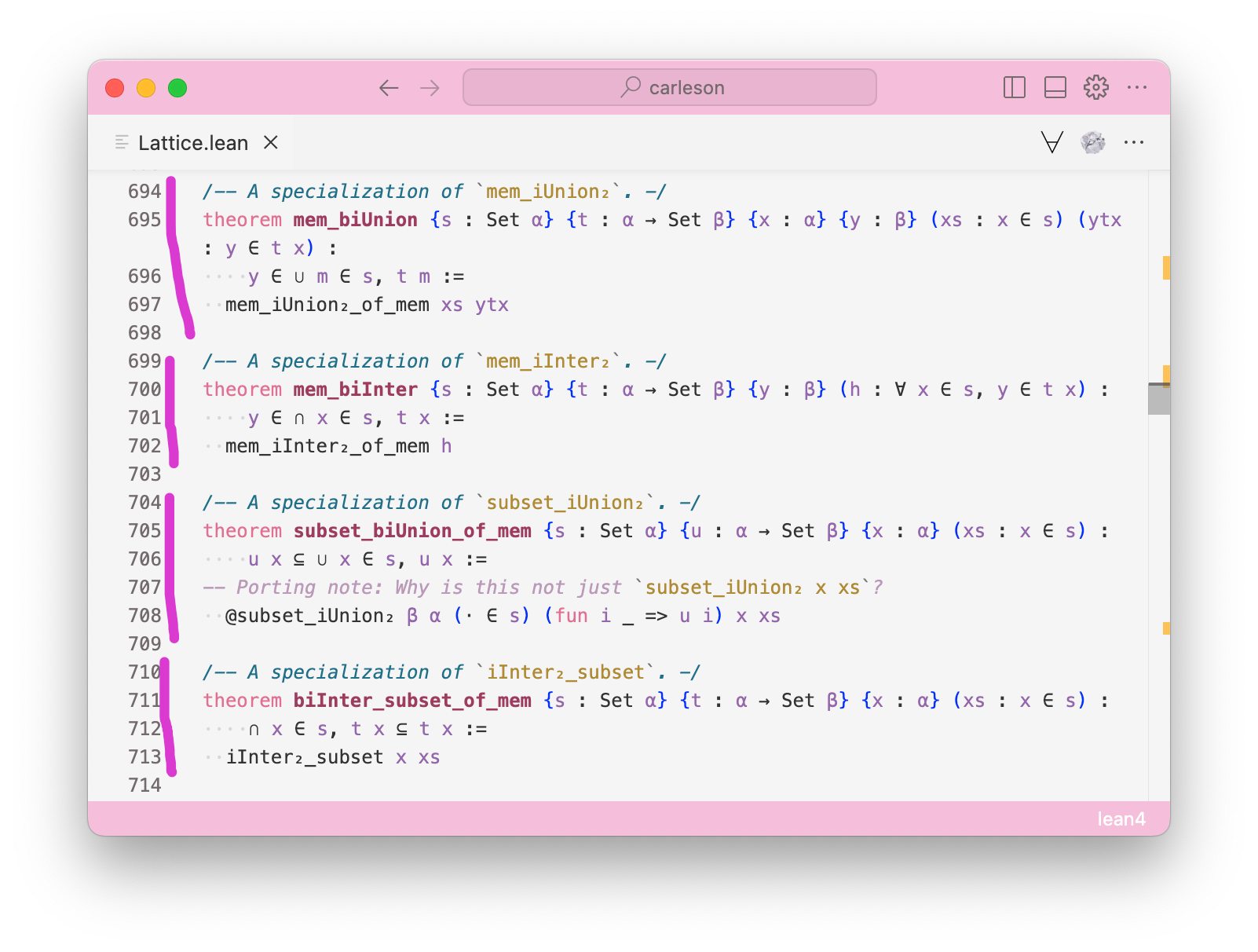
Snapshot of the theorem mem_biUnion starts at line 694 and ends at line 697.Given a line number and a character number, we can determine the relevant Snapshot. For example, withWaitFindSnapAtPos { line: 708, character 20 } λ snapshot => do {} will return the snapshot for the subset_biUnion_of_mem theorem, just like any other line & character combination within that theorem.
Request handlers usually locate and access a single snapshot in the tree based on the cursor position using withWaitFindSnap, which will wait for elaboration if it is not sufficiently progressed yet. After the snapshot is available, they can access its data, in particular the command's Syntax tree and elaboration InfoTree, in order to respond to the request.
(From github.com/leanprover/lean4/blob/master/src/Lean/Server/README.md)
The Snapshot object, in its turn, has snapshot.infoTree field, which gives us the InfoTree object. It contains a list of tactics, and all goals and hypotheses before and after each tactic was applied. To quote the docs again:
The InfoTree is the second central server metadata structure. It is filled during elaboration with various metadata that cannot (easily) be recovered from the kernel declarations in the environment: goal & subterm infos including the precise local & metavariable contexts used during elaboration, macro expansion steps, etc. Once a relevant Snapshot
snaphas been located,snap.infoTree.smallestInfo?and other functions fromLean.Server.InfoUtilscan be used to further locate information about a document position. The commandset_option trace.Elab.info trueinstructs Lean to display the InfoTree for the declarations occurring after it.
(From github.com/leanprover/lean4/blob/master/src/Lean/Server/README.md)
Data structures
Suppose we're parsing the following theorem in Paperproof:
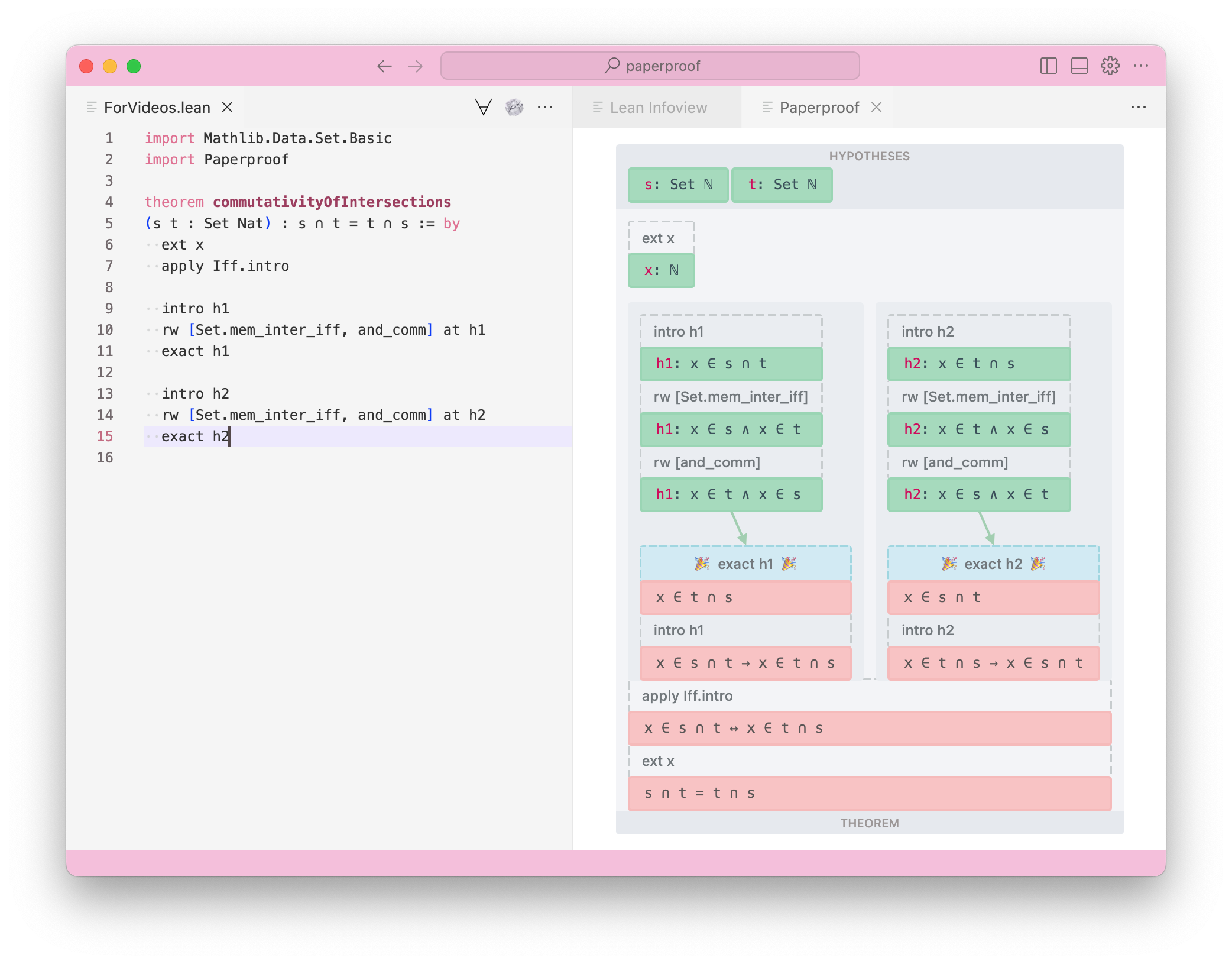
If you pretty-print the InfoTree of this proof, you'll get the following 3.5k-line output:
Click to expand JSON
• command @ ⟨4, 0⟩-⟨15, 10⟩ @ Lean.Elab.Command.elabDeclaration
• Set ℕ : Type @ ⟨5, 7⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabApp
• [.] Set : some Sort.{?_uniq.1} @ ⟨5, 7⟩-⟨5, 10⟩
• Set : Type → Type @ ⟨5, 7⟩-⟨5, 10⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabIdent
• [.] Nat : some Type.{?_uniq.2} @ ⟨5, 11⟩-⟨5, 14⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩
• s (isBinder := true) : Set ℕ @ ⟨5, 1⟩-⟨5, 2⟩
• Set ℕ : Type @ ⟨5, 7⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabApp
• [.] Set : some Sort.{?_uniq.4} @ ⟨5, 7⟩-⟨5, 10⟩
• Set : Type → Type @ ⟨5, 7⟩-⟨5, 10⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabIdent
• [.] Nat : some Type.{?_uniq.5} @ ⟨5, 11⟩-⟨5, 14⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩
• t (isBinder := true) : Set ℕ @ ⟨5, 3⟩-⟨5, 4⟩
• s ∩ t = t ∩ s : Prop @ ⟨5, 18⟩-⟨5, 31⟩ @ «_aux_Init_Notation___macroRules_term_=__2»
• Macro expansion
s ∩ t = t ∩ s
===>
binrel% Eq✝ (s ∩ t) (t ∩ s)
• s ∩ t = t ∩ s : Prop @ ⟨5, 18⟩†-⟨5, 31⟩† @ Lean.Elab.Term.Op.elabBinRel
• s ∩ t = t ∩ s : Prop @ ⟨5, 18⟩†-⟨5, 31⟩†
• s ∩ t : Set ℕ @ ⟨5, 18⟩-⟨5, 23⟩ @ «_aux_Init_Core___macroRules_term_∩__1»
• Macro expansion
s ∩ t
===>
Inter.inter✝ s t
• [.] Eq✝ : none @ ⟨5, 18⟩†-⟨5, 31⟩†
• s ∩ t : Set ℕ @ ⟨5, 18⟩†-⟨5, 23⟩† @ Lean.Elab.Term.elabApp
• [.] Inter.inter✝ : none @ ⟨5, 18⟩†-⟨5, 23⟩†
• @Inter.inter : {α : Type} → [self : Inter α] → α → α → α @ ⟨5, 18⟩†-⟨5, 23⟩†
• s : Set ℕ @ ⟨5, 18⟩-⟨5, 19⟩ @ Lean.Elab.Term.elabIdent
• [.] s : some ?_uniq.10 @ ⟨5, 18⟩-⟨5, 19⟩
• s : Set ℕ @ ⟨5, 18⟩-⟨5, 19⟩
• t : Set ℕ @ ⟨5, 22⟩-⟨5, 23⟩ @ Lean.Elab.Term.elabIdent
• [.] t : some ?_uniq.10 @ ⟨5, 22⟩-⟨5, 23⟩
• t : Set ℕ @ ⟨5, 22⟩-⟨5, 23⟩
• t ∩ s : Set ℕ @ ⟨5, 26⟩-⟨5, 31⟩ @ «_aux_Init_Core___macroRules_term_∩__1»
• Macro expansion
t ∩ s
===>
Inter.inter✝ t s
• t ∩ s : Set ℕ @ ⟨5, 26⟩†-⟨5, 31⟩† @ Lean.Elab.Term.elabApp
• [.] Inter.inter✝ : none @ ⟨5, 26⟩†-⟨5, 31⟩†
• @Inter.inter : {α : Type} → [self : Inter α] → α → α → α @ ⟨5, 26⟩†-⟨5, 31⟩†
• t : Set ℕ @ ⟨5, 26⟩-⟨5, 27⟩ @ Lean.Elab.Term.elabIdent
• [.] t : some ?_uniq.23 @ ⟨5, 26⟩-⟨5, 27⟩
• t : Set ℕ @ ⟨5, 26⟩-⟨5, 27⟩
• s : Set ℕ @ ⟨5, 30⟩-⟨5, 31⟩ @ Lean.Elab.Term.elabIdent
• [.] s : some ?_uniq.23 @ ⟨5, 30⟩-⟨5, 31⟩
• s : Set ℕ @ ⟨5, 30⟩-⟨5, 31⟩
• commutativityOfIntersections (isBinder := true) : ∀ (s t : Set ℕ), s ∩ t = t ∩ s @ ⟨4, 8⟩-⟨4, 36⟩
• s (isBinder := true) : Set ℕ @ ⟨5, 1⟩-⟨5, 2⟩
• t (isBinder := true) : Set ℕ @ ⟨5, 3⟩-⟨5, 4⟩
• Tactic @ ⟨5, 35⟩-⟨15, 10⟩
(Term.byTactic
"by"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
[]
(Tactic.apply "apply" `Iff.intro)
[]
(Tactic.intro "intro" [`h1])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
[]
(Tactic.exact "exact" `h1)
[]
(Tactic.intro "intro" [`h2])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
[]
(Tactic.exact "exact" `h2)])))
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨5, 35⟩-⟨5, 37⟩
"by"
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨6, 2⟩-⟨15, 10⟩ @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
[]
(Tactic.apply "apply" `Iff.intro)
[]
(Tactic.intro "intro" [`h1])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
[]
(Tactic.exact "exact" `h1)
[]
(Tactic.intro "intro" [`h2])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
[]
(Tactic.exact "exact" `h2)]))
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨6, 2⟩-⟨15, 10⟩ @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
[]
(Tactic.apply "apply" `Iff.intro)
[]
(Tactic.intro "intro" [`h1])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
[]
(Tactic.exact "exact" `h1)
[]
(Tactic.intro "intro" [`h2])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
[]
(Tactic.exact "exact" `h2)])
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨6, 2⟩-⟨6, 7⟩ @ Lean.Elab.Tactic.Ext.evalExt
(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after
case h
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t ↔ x ∈ t ∩ s
• x (isBinder := true) : ℕ @ ⟨6, 6⟩-⟨6, 7⟩
• Tactic @ ⟨7, 2⟩-⟨7, 17⟩ @ Lean.Elab.Tactic.evalApply
(Tactic.apply "apply" `Iff.intro)
before
case h
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t ↔ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t → x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• [.] Iff.intro : none @ ⟨7, 8⟩-⟨7, 17⟩
• @Iff.intro : ∀ {a b : Prop}, (a → b) → (b → a) → (a ↔ b) @ ⟨7, 8⟩-⟨7, 17⟩
• Tactic @ ⟨9, 2⟩-⟨9, 10⟩ @ Lean.Elab.Tactic.evalIntro
(Tactic.intro "intro" [`h1])
before
case h.mp
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t → x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• h1 (isBinder := true) : x ∈ s ∩ t @ ⟨9, 8⟩-⟨9, 10⟩
• Tactic @ ⟨10, 2⟩-⟨10, 40⟩ @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_rwSeq_1
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
")")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
["rewrite" "["]
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 6⟩-⟨10, 24⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `Set.mem_inter_iff) ","]
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∧ x ∈ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• [.] Set.mem_inter_iff : none @ ⟨10, 6⟩-⟨10, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type ?u.71} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨10, 6⟩-⟨10, 23⟩
• [.] h1 : none @ ⟨10, 38⟩-⟨10, 40⟩
• h1 : x ∈ s ∩ t @ ⟨10, 38⟩-⟨10, 40⟩
• Set.mem_inter_iff : ∀ (x : ℕ) (a b : Set ℕ),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨10, 6⟩-⟨10, 23⟩ @ Lean.Elab.Term.elabIdent
• [.] Set.mem_inter_iff : none @ ⟨10, 6⟩-⟨10, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨10, 6⟩-⟨10, 23⟩
• Tactic @ ⟨10, 25⟩-⟨10, 33⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `and_comm) ]
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∧ x ∈ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• [.] and_comm : none @ ⟨10, 25⟩-⟨10, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨10, 25⟩-⟨10, 33⟩
• [.] h1 : none @ ⟨10, 38⟩-⟨10, 40⟩
• h1 : x ∈ s ∧ x ∈ t @ ⟨10, 38⟩-⟨10, 40⟩
• and_comm : x ∈ s ∧ x ∈ t ↔ x ∈ t ∧ x ∈ s @ ⟨10, 25⟩-⟨10, 33⟩ @ Lean.Elab.Term.elabIdent
• [.] and_comm : none @ ⟨10, 25⟩-⟨10, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨10, 25⟩-⟨10, 33⟩
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
";"
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalWithAnnotateState
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 33⟩-⟨10, 34⟩ @ Lean.Elab.Tactic.evalWithAnnotateState
"]"
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticTry__1
(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalFirst
(Tactic.first
"first"
[(group
"|"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
(group "|" (Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")])))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalWithReducible
(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticRfl_1
(Tactic.tacticRfl "rfl")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalCase'
(Tactic.case'
"case'"
[(Tactic.caseArg (Lean.binderIdent (Term.hole "_")) [])]
"=>"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalFail
(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.skip "skip")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalSkip
(Tactic.skip "skip")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨11, 2⟩-⟨11, 10⟩ @ Lean.Elab.Tactic.evalExact
(Tactic.exact "exact" `h1)
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• h1 : x ∈ t ∧ x ∈ s @ ⟨11, 8⟩-⟨11, 10⟩ @ Lean.Elab.Term.elabIdent
• [.] h1 : some Membership.mem.{0, 0} Nat (Set.{0} Nat) (Set.instMembership.{0} Nat) (Inter.inter.{0} (Set.{0} Nat) (Set.instInter.{0} Nat) _uniq.31 _uniq.30) _uniq.55 @ ⟨11, 8⟩-⟨11, 10⟩
• h1 : x ∈ t ∧ x ∈ s @ ⟨11, 8⟩-⟨11, 10⟩
• Tactic @ ⟨13, 2⟩-⟨13, 10⟩ @ Lean.Elab.Tactic.evalIntro
(Tactic.intro "intro" [`h2])
before
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
• h2 (isBinder := true) : x ∈ t ∩ s @ ⟨13, 8⟩-⟨13, 10⟩
• Tactic @ ⟨14, 2⟩-⟨14, 40⟩ @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_rwSeq_1
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
")")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
["rewrite" "["]
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 6⟩-⟨14, 24⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `Set.mem_inter_iff) ","]
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∧ x ∈ s
⊢ x ∈ s ∩ t
• [.] Set.mem_inter_iff : none @ ⟨14, 6⟩-⟨14, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type ?u.127} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨14, 6⟩-⟨14, 23⟩
• [.] h2 : none @ ⟨14, 38⟩-⟨14, 40⟩
• h2 : x ∈ t ∩ s @ ⟨14, 38⟩-⟨14, 40⟩
• Set.mem_inter_iff : ∀ (x : ℕ) (a b : Set ℕ),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨14, 6⟩-⟨14, 23⟩ @ Lean.Elab.Term.elabIdent
• [.] Set.mem_inter_iff : none @ ⟨14, 6⟩-⟨14, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨14, 6⟩-⟨14, 23⟩
• Tactic @ ⟨14, 25⟩-⟨14, 33⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `and_comm) ]
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∧ x ∈ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• [.] and_comm : none @ ⟨14, 25⟩-⟨14, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨14, 25⟩-⟨14, 33⟩
• [.] h2 : none @ ⟨14, 38⟩-⟨14, 40⟩
• h2 : x ∈ t ∧ x ∈ s @ ⟨14, 38⟩-⟨14, 40⟩
• and_comm : x ∈ t ∧ x ∈ s ↔ x ∈ s ∧ x ∈ t @ ⟨14, 25⟩-⟨14, 33⟩ @ Lean.Elab.Term.elabIdent
• [.] and_comm : none @ ⟨14, 25⟩-⟨14, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨14, 25⟩-⟨14, 33⟩
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
";"
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalWithAnnotateState
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 33⟩-⟨14, 34⟩ @ Lean.Elab.Tactic.evalWithAnnotateState
"]"
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticTry__1
(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalFirst
(Tactic.first
"first"
[(group
"|"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
(group "|" (Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")])))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalWithReducible
(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticRfl_1
(Tactic.tacticRfl "rfl")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalCase'
(Tactic.case'
"case'"
[(Tactic.caseArg (Lean.binderIdent (Term.hole "_")) [])]
"=>"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalFail
(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.skip "skip")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalSkip
(Tactic.skip "skip")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨15, 2⟩-⟨15, 10⟩ @ Lean.Elab.Tactic.evalExact
(Tactic.exact "exact" `h2)
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after no goals
• h2 : x ∈ s ∧ x ∈ t @ ⟨15, 8⟩-⟨15, 10⟩ @ Lean.Elab.Term.elabIdent
• [.] h2 : some Membership.mem.{0, 0} Nat (Set.{0} Nat) (Set.instMembership.{0} Nat) (Inter.inter.{0} (Set.{0} Nat) (Set.instInter.{0} Nat) _uniq.30 _uniq.31) _uniq.55 @ ⟨15, 8⟩-⟨15, 10⟩
• h2 : x ∈ s ∧ x ∈ t @ ⟨15, 8⟩-⟨15, 10⟩
• commutativityOfIntersections (isBinder := true) : ∀ (s t : Set ℕ), s ∩ t = t ∩ s @ ⟨4, 8⟩-⟨4, 36⟩
• command @ ⟨4, 0⟩-⟨15, 10⟩ @ Lean.Elab.Command.elabDeclaration
• Set ℕ : Type @ ⟨5, 7⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabApp
• [.] Set : some Sort.{?_uniq.1} @ ⟨5, 7⟩-⟨5, 10⟩
• Set : Type → Type @ ⟨5, 7⟩-⟨5, 10⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabIdent
• [.] Nat : some Type.{?_uniq.2} @ ⟨5, 11⟩-⟨5, 14⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩
• s (isBinder := true) : Set ℕ @ ⟨5, 1⟩-⟨5, 2⟩
• Set ℕ : Type @ ⟨5, 7⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabApp
• [.] Set : some Sort.{?_uniq.4} @ ⟨5, 7⟩-⟨5, 10⟩
• Set : Type → Type @ ⟨5, 7⟩-⟨5, 10⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩ @ Lean.Elab.Term.elabIdent
• [.] Nat : some Type.{?_uniq.5} @ ⟨5, 11⟩-⟨5, 14⟩
• ℕ : Type @ ⟨5, 11⟩-⟨5, 14⟩
• t (isBinder := true) : Set ℕ @ ⟨5, 3⟩-⟨5, 4⟩
• s ∩ t = t ∩ s : Prop @ ⟨5, 18⟩-⟨5, 31⟩ @ «_aux_Init_Notation___macroRules_term_=__2»
• Macro expansion
s ∩ t = t ∩ s
===>
binrel% Eq✝ (s ∩ t) (t ∩ s)
• s ∩ t = t ∩ s : Prop @ ⟨5, 18⟩†-⟨5, 31⟩† @ Lean.Elab.Term.Op.elabBinRel
• s ∩ t = t ∩ s : Prop @ ⟨5, 18⟩†-⟨5, 31⟩†
• s ∩ t : Set ℕ @ ⟨5, 18⟩-⟨5, 23⟩ @ «_aux_Init_Core___macroRules_term_∩__1»
• Macro expansion
s ∩ t
===>
Inter.inter✝ s t
• [.] Eq✝ : none @ ⟨5, 18⟩†-⟨5, 31⟩†
• s ∩ t : Set ℕ @ ⟨5, 18⟩†-⟨5, 23⟩† @ Lean.Elab.Term.elabApp
• [.] Inter.inter✝ : none @ ⟨5, 18⟩†-⟨5, 23⟩†
• @Inter.inter : {α : Type} → [self : Inter α] → α → α → α @ ⟨5, 18⟩†-⟨5, 23⟩†
• s : Set ℕ @ ⟨5, 18⟩-⟨5, 19⟩ @ Lean.Elab.Term.elabIdent
• [.] s : some ?_uniq.10 @ ⟨5, 18⟩-⟨5, 19⟩
• s : Set ℕ @ ⟨5, 18⟩-⟨5, 19⟩
• t : Set ℕ @ ⟨5, 22⟩-⟨5, 23⟩ @ Lean.Elab.Term.elabIdent
• [.] t : some ?_uniq.10 @ ⟨5, 22⟩-⟨5, 23⟩
• t : Set ℕ @ ⟨5, 22⟩-⟨5, 23⟩
• t ∩ s : Set ℕ @ ⟨5, 26⟩-⟨5, 31⟩ @ «_aux_Init_Core___macroRules_term_∩__1»
• Macro expansion
t ∩ s
===>
Inter.inter✝ t s
• t ∩ s : Set ℕ @ ⟨5, 26⟩†-⟨5, 31⟩† @ Lean.Elab.Term.elabApp
• [.] Inter.inter✝ : none @ ⟨5, 26⟩†-⟨5, 31⟩†
• @Inter.inter : {α : Type} → [self : Inter α] → α → α → α @ ⟨5, 26⟩†-⟨5, 31⟩†
• t : Set ℕ @ ⟨5, 26⟩-⟨5, 27⟩ @ Lean.Elab.Term.elabIdent
• [.] t : some ?_uniq.23 @ ⟨5, 26⟩-⟨5, 27⟩
• t : Set ℕ @ ⟨5, 26⟩-⟨5, 27⟩
• s : Set ℕ @ ⟨5, 30⟩-⟨5, 31⟩ @ Lean.Elab.Term.elabIdent
• [.] s : some ?_uniq.23 @ ⟨5, 30⟩-⟨5, 31⟩
• s : Set ℕ @ ⟨5, 30⟩-⟨5, 31⟩
• commutativityOfIntersections (isBinder := true) : ∀ (s t : Set ℕ), s ∩ t = t ∩ s @ ⟨4, 8⟩-⟨4, 36⟩
• s (isBinder := true) : Set ℕ @ ⟨5, 1⟩-⟨5, 2⟩
• t (isBinder := true) : Set ℕ @ ⟨5, 3⟩-⟨5, 4⟩
• Tactic @ ⟨5, 35⟩-⟨15, 10⟩
(Term.byTactic
"by"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
[]
(Tactic.apply "apply" `Iff.intro)
[]
(Tactic.intro "intro" [`h1])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
[]
(Tactic.exact "exact" `h1)
[]
(Tactic.intro "intro" [`h2])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
[]
(Tactic.exact "exact" `h2)])))
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨5, 35⟩-⟨5, 37⟩
"by"
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨6, 2⟩-⟨15, 10⟩ @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
[]
(Tactic.apply "apply" `Iff.intro)
[]
(Tactic.intro "intro" [`h1])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
[]
(Tactic.exact "exact" `h1)
[]
(Tactic.intro "intro" [`h2])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
[]
(Tactic.exact "exact" `h2)]))
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨6, 2⟩-⟨15, 10⟩ @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
[]
(Tactic.apply "apply" `Iff.intro)
[]
(Tactic.intro "intro" [`h1])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
[]
(Tactic.exact "exact" `h1)
[]
(Tactic.intro "intro" [`h2])
[]
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
[]
(Tactic.exact "exact" `h2)])
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after no goals
• Tactic @ ⟨6, 2⟩-⟨6, 7⟩ @ Lean.Elab.Tactic.Ext.evalExt
(Lean.Elab.Tactic.Ext.ext "ext" [(Tactic.rintroPat.one (Tactic.rcasesPat.one `x))] [])
before
s t : Set ℕ
⊢ s ∩ t = t ∩ s
after
case h
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t ↔ x ∈ t ∩ s
• x (isBinder := true) : ℕ @ ⟨6, 6⟩-⟨6, 7⟩
• Tactic @ ⟨7, 2⟩-⟨7, 17⟩ @ Lean.Elab.Tactic.evalApply
(Tactic.apply "apply" `Iff.intro)
before
case h
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t ↔ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t → x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• [.] Iff.intro : none @ ⟨7, 8⟩-⟨7, 17⟩
• @Iff.intro : ∀ {a b : Prop}, (a → b) → (b → a) → (a ↔ b) @ ⟨7, 8⟩-⟨7, 17⟩
• Tactic @ ⟨9, 2⟩-⟨9, 10⟩ @ Lean.Elab.Tactic.evalIntro
(Tactic.intro "intro" [`h1])
before
case h.mp
s t : Set ℕ
x : ℕ
⊢ x ∈ s ∩ t → x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• h1 (isBinder := true) : x ∈ s ∩ t @ ⟨9, 8⟩-⟨9, 10⟩
• Tactic @ ⟨10, 2⟩-⟨10, 40⟩ @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_rwSeq_1
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
")")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h1] []))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
["rewrite" "["]
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 6⟩-⟨10, 24⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `Set.mem_inter_iff) ","]
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∩ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∧ x ∈ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• [.] Set.mem_inter_iff : none @ ⟨10, 6⟩-⟨10, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type ?u.71} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨10, 6⟩-⟨10, 23⟩
• [.] h1 : none @ ⟨10, 38⟩-⟨10, 40⟩
• h1 : x ∈ s ∩ t @ ⟨10, 38⟩-⟨10, 40⟩
• Set.mem_inter_iff : ∀ (x : ℕ) (a b : Set ℕ),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨10, 6⟩-⟨10, 23⟩ @ Lean.Elab.Term.elabIdent
• [.] Set.mem_inter_iff : none @ ⟨10, 6⟩-⟨10, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨10, 6⟩-⟨10, 23⟩
• Tactic @ ⟨10, 25⟩-⟨10, 33⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `and_comm) ]
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ s ∧ x ∈ t
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• [.] and_comm : none @ ⟨10, 25⟩-⟨10, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨10, 25⟩-⟨10, 33⟩
• [.] h1 : none @ ⟨10, 38⟩-⟨10, 40⟩
• h1 : x ∈ s ∧ x ∈ t @ ⟨10, 38⟩-⟨10, 40⟩
• and_comm : x ∈ s ∧ x ∈ t ↔ x ∈ t ∧ x ∈ s @ ⟨10, 25⟩-⟨10, 33⟩ @ Lean.Elab.Term.elabIdent
• [.] and_comm : none @ ⟨10, 25⟩-⟨10, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨10, 25⟩-⟨10, 33⟩
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
";"
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalWithAnnotateState
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 33⟩-⟨10, 34⟩ @ Lean.Elab.Tactic.evalWithAnnotateState
"]"
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticTry__1
(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalFirst
(Tactic.first
"first"
[(group
"|"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
(group "|" (Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")])))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalWithReducible
(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticRfl_1
(Tactic.tacticRfl "rfl")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalCase'
(Tactic.case'
"case'"
[(Tactic.caseArg (Lean.binderIdent (Term.hole "_")) [])]
"=>"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalFail
(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")]))
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.skip "skip")])
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨10, 2⟩†-⟨10, 40⟩† @ Lean.Elab.Tactic.evalSkip
(Tactic.skip "skip")
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• Tactic @ ⟨11, 2⟩-⟨11, 10⟩ @ Lean.Elab.Tactic.evalExact
(Tactic.exact "exact" `h1)
before
case h.mp
s t : Set ℕ
x : ℕ
h1 : x ∈ t ∧ x ∈ s
⊢ x ∈ t ∩ s
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
• h1 : x ∈ t ∧ x ∈ s @ ⟨11, 8⟩-⟨11, 10⟩ @ Lean.Elab.Term.elabIdent
• [.] h1 : some Membership.mem.{0, 0} Nat (Set.{0} Nat) (Set.instMembership.{0} Nat) (Inter.inter.{0} (Set.{0} Nat) (Set.instInter.{0} Nat) _uniq.31 _uniq.30) _uniq.55 @ ⟨11, 8⟩-⟨11, 10⟩
• h1 : x ∈ t ∧ x ∈ s @ ⟨11, 8⟩-⟨11, 10⟩
• Tactic @ ⟨13, 2⟩-⟨13, 10⟩ @ Lean.Elab.Tactic.evalIntro
(Tactic.intro "intro" [`h2])
before
case h.mpr
s t : Set ℕ
x : ℕ
⊢ x ∈ t ∩ s → x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
• h2 (isBinder := true) : x ∈ t ∩ s @ ⟨13, 8⟩-⟨13, 10⟩
• Tactic @ ⟨14, 2⟩-⟨14, 40⟩ @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_rwSeq_1
(Tactic.rwSeq
"rw"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
")")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
";"
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
(Tactic.rewriteSeq
"rewrite"
[]
(Tactic.rwRuleSeq "[" [(Tactic.rwRule [] `Set.mem_inter_iff) "," (Tactic.rwRule [] `and_comm)] "]")
[(Tactic.location "at" (Tactic.locationHyp [`h2] []))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalRewriteSeq
["rewrite" "["]
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 6⟩-⟨14, 24⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `Set.mem_inter_iff) ","]
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∩ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∧ x ∈ s
⊢ x ∈ s ∩ t
• [.] Set.mem_inter_iff : none @ ⟨14, 6⟩-⟨14, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type ?u.127} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨14, 6⟩-⟨14, 23⟩
• [.] h2 : none @ ⟨14, 38⟩-⟨14, 40⟩
• h2 : x ∈ t ∩ s @ ⟨14, 38⟩-⟨14, 40⟩
• Set.mem_inter_iff : ∀ (x : ℕ) (a b : Set ℕ),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨14, 6⟩-⟨14, 23⟩ @ Lean.Elab.Term.elabIdent
• [.] Set.mem_inter_iff : none @ ⟨14, 6⟩-⟨14, 23⟩
• @Set.mem_inter_iff : ∀ {α : Type} (x : α) (a b : Set α),
x ∈ a ∩ b ↔ x ∈ a ∧ x ∈ b @ ⟨14, 6⟩-⟨14, 23⟩
• Tactic @ ⟨14, 25⟩-⟨14, 33⟩ @ Lean.Elab.Tactic.evalRewriteSeq
[(Tactic.rwRule [] `and_comm) ]
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ t ∧ x ∈ s
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• [.] and_comm : none @ ⟨14, 25⟩-⟨14, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨14, 25⟩-⟨14, 33⟩
• [.] h2 : none @ ⟨14, 38⟩-⟨14, 40⟩
• h2 : x ∈ t ∧ x ∈ s @ ⟨14, 38⟩-⟨14, 40⟩
• and_comm : x ∈ t ∧ x ∈ s ↔ x ∈ s ∧ x ∈ t @ ⟨14, 25⟩-⟨14, 33⟩ @ Lean.Elab.Term.elabIdent
• [.] and_comm : none @ ⟨14, 25⟩-⟨14, 33⟩
• @and_comm : ∀ {a b : Prop}, a ∧ b ↔ b ∧ a @ ⟨14, 25⟩-⟨14, 33⟩
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
";"
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalWithAnnotateState
(Tactic.withAnnotateState
"with_annotate_state"
"]"
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")"))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 33⟩-⟨14, 34⟩ @ Lean.Elab.Tactic.evalWithAnnotateState
"]"
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
")")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticTry__1
(Tactic.tacticTry_
"try"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalFirst
(Tactic.first
"first"
[(group
"|"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])))
(group "|" (Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")])))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalParen
(Tactic.paren
"("
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
")")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalWithReducible
(Tactic.withReducible
"with_reducible"
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.tacticRfl "rfl")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Parser.Tactic._aux_Init_Tactics___macroRules_Lean_Parser_Tactic_tacticRfl_1
(Tactic.tacticRfl "rfl")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalCase'
(Tactic.case'
"case'"
[(Tactic.caseArg (Lean.binderIdent (Term.hole "_")) [])]
"=>"
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented
[(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalFail
(Tactic.fail
"fail"
[(str
"\"The rfl tactic failed. Possible reasons:\n- The goal is not a reflexive relation (neither `=` nor a relation with a @[refl] lemma).\n- The arguments of the relation are not equal.\nTry using the reflexivity lemma for your relation explicitly, e.g. `exact Eq.refl _` or\n`exact HEq.rfl` etc.\"")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq
(Tactic.tacticSeq (Tactic.tacticSeq1Indented [(Tactic.skip "skip")]))
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalTacticSeq1Indented
(Tactic.tacticSeq1Indented [(Tactic.skip "skip")])
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨14, 2⟩†-⟨14, 40⟩† @ Lean.Elab.Tactic.evalSkip
(Tactic.skip "skip")
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
• Tactic @ ⟨15, 2⟩-⟨15, 10⟩ @ Lean.Elab.Tactic.evalExact
(Tactic.exact "exact" `h2)
before
case h.mpr
s t : Set ℕ
x : ℕ
h2 : x ∈ s ∧ x ∈ t
⊢ x ∈ s ∩ t
after no goals
• h2 : x ∈ s ∧ x ∈ t @ ⟨15, 8⟩-⟨15, 10⟩ @ Lean.Elab.Term.elabIdent
• [.] h2 : some Membership.mem.{0, 0} Nat (Set.{0} Nat) (Set.instMembership.{0} Nat) (Inter.inter.{0} (Set.{0} Nat) (Set.instInter.{0} Nat) _uniq.30 _uniq.31) _uniq.55 @ ⟨15, 8⟩-⟨15, 10⟩
• h2 : x ∈ s ∧ x ∈ t @ ⟨15, 8⟩-⟨15, 10⟩
• commutativityOfIntersections (isBinder := true) : ∀ (s t : Set ℕ), s ∩ t = t ∩ s @ ⟨4, 8⟩-⟨4, 36⟩
We feed this InfoTree into our BetterParser.lean (github.com/Paper-Proof/paperproof/.../BetterParser.lean), which results in the following data structure:
Click to expand JSON
[
{
"tacticString": "ext x",
"tacticDependsOn": [],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h",
"type": "x ∈ s ∩ t ↔ x ∈ t ∩ s",
"id": "_uniq.56",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"}
]
}
],
"goalBefore": {
"username": "[anonymous]",
"type": "s ∩ t = t ∩ s",
"id": "_uniq.32",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"}
]
}
},
{
"tacticString": "apply Iff.intro",
"tacticDependsOn": [],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h.mp",
"type": "x ∈ s ∩ t → x ∈ t ∩ s",
"id": "_uniq.64",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"}
]
},
{
"username": "h.mpr",
"type": "x ∈ t ∩ s → x ∈ s ∩ t",
"id": "_uniq.65",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"}
]
}
],
"goalBefore": {
"username": "h",
"type": "x ∈ s ∩ t ↔ x ∈ t ∩ s",
"id": "_uniq.56",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"}
]
}
},
{
"tacticString": "intro h1",
"tacticDependsOn": [],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h.mp",
"type": "x ∈ t ∩ s",
"id": "_uniq.69",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h1", "type": "x ∈ s ∩ t", "isProof": "proof", "id": "_uniq.68"}
]
}
],
"goalBefore": {
"username": "h.mp",
"type": "x ∈ s ∩ t → x ∈ t ∩ s",
"id": "_uniq.64",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"}
]
}
},
{
"tacticString": "rw [Set.mem_inter_iff]",
"tacticDependsOn": ["_uniq.68"],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h.mp",
"type": "x ∈ t ∩ s",
"id": "_uniq.102",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h1", "type": "x ∈ s ∧ x ∈ t", "isProof": "proof", "id": "_uniq.99"}
]
}
],
"goalBefore": {
"username": "h.mp",
"type": "x ∈ t ∩ s",
"id": "_uniq.69",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h1", "type": "x ∈ s ∩ t", "isProof": "proof", "id": "_uniq.68"}
]
}
},
{
"tacticString": "rw [and_comm]",
"tacticDependsOn": ["_uniq.99"],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h.mp",
"type": "x ∈ t ∩ s",
"id": "_uniq.119",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h1", "type": "x ∈ t ∧ x ∈ s", "isProof": "proof", "id": "_uniq.116"}
]
}
],
"goalBefore": {
"username": "h.mp",
"type": "x ∈ t ∩ s",
"id": "_uniq.102",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h1", "type": "x ∈ s ∧ x ∈ t", "isProof": "proof", "id": "_uniq.99"}
]
}
},
{
"tacticString": "exact h1",
"tacticDependsOn": ["_uniq.116"],
"spawnedGoals": [],
"goalsAfter": [],
"goalBefore": {
"username": "h.mp",
"type": "x ∈ t ∩ s",
"id": "_uniq.119",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h1", "type": "x ∈ t ∧ x ∈ s", "isProof": "proof", "id": "_uniq.116"}
]
}
},
{
"tacticString": "intro h2",
"tacticDependsOn": [],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h.mpr",
"type": "x ∈ s ∩ t",
"id": "_uniq.125",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h2", "type": "x ∈ t ∩ s", "isProof": "proof", "id": "_uniq.124"}
]
}
],
"goalBefore": {
"username": "h.mpr",
"type": "x ∈ t ∩ s → x ∈ s ∩ t",
"id": "_uniq.65",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"}
]
}
},
{
"tacticString": "rw [Set.mem_inter_iff]",
"tacticDependsOn": ["_uniq.124"],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h.mpr",
"type": "x ∈ s ∩ t",
"id": "_uniq.148",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h2", "type": "x ∈ t ∧ x ∈ s", "isProof": "proof", "id": "_uniq.145"}
]
}
],
"goalBefore": {
"username": "h.mpr",
"type": "x ∈ s ∩ t",
"id": "_uniq.125",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h2", "type": "x ∈ t ∩ s", "isProof": "proof", "id": "_uniq.124"}
]
}
},
{
"tacticString": "rw [and_comm]",
"tacticDependsOn": ["_uniq.145"],
"spawnedGoals": [],
"goalsAfter": [
{
"username": "h.mpr",
"type": "x ∈ s ∩ t",
"id": "_uniq.163",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h2", "type": "x ∈ s ∧ x ∈ t", "isProof": "proof", "id": "_uniq.160"}
]
}
],
"goalBefore": {
"username": "h.mpr",
"type": "x ∈ s ∩ t",
"id": "_uniq.148",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h2", "type": "x ∈ t ∧ x ∈ s", "isProof": "proof", "id": "_uniq.145"}
]
}
},
{
"tacticString": "exact h2",
"tacticDependsOn": ["_uniq.160"],
"spawnedGoals": [],
"goalsAfter": [],
"goalBefore": {
"username": "h.mpr",
"type": "x ∈ s ∩ t",
"id": "_uniq.163",
"hyps": [
{"value": null, "username": "s", "type": "Set ℕ", "isProof": "data", "id": "_uniq.30"},
{"value": null, "username": "t", "type": "Set ℕ", "isProof": "data", "id": "_uniq.31"},
{"value": null, "username": "x", "type": "ℕ", "isProof": "data", "id": "_uniq.55"},
{"value": null, "username": "h2", "type": "x ∈ s ∧ x ∈ t", "isProof": "proof", "id": "_uniq.160"}
]
}
}
]
This is returned as JSON to the webview. In the webview, we do some more data preparation - this time using converter.ts (github.com/Paper-Proof/paperproof/.../converter.ts), which results in the following data structure:
Click to expand JSON
{
"boxes": [
{
"id": "1",
"parentId": null,
"goalNodes": [
{"text": "s ∩ t = t ∩ s", "name": "[anonymous]", "id": "_uniq.32"},
{"text": "x ∈ s ∩ t ↔ x ∈ t ∩ s", "name": "h", "id": "_uniq.56"}
],
"hypLayers": [
{
"tacticId": "1",
"hypNodes": [
{"text": "Set ℕ", "name": "s", "id": "_uniq.30", "isProof": "data"},
{"text": "Set ℕ", "name": "t", "id": "_uniq.31", "isProof": "data"}
]
},
{
"tacticId": "2",
"hypNodes": [
{"text": "ℕ", "name": "x", "id": "_uniq.55", "isProof": "data"}
]
}
],
"hypTables": []
},
{
"id": "2",
"parentId": "1",
"goalNodes": [
{"text": "x ∈ s ∩ t → x ∈ t ∩ s", "name": "h.mp", "id": "_uniq.64"},
{"text": "x ∈ t ∩ s", "name": "h.mp", "id": "_uniq.69"}
],
"hypLayers": [
{
"tacticId": "4",
"hypNodes": [
{"text": "x ∈ s ∩ t", "name": "h1", "id": "_uniq.68", "isProof": "proof"}
]
},
{
"tacticId": "5",
"hypNodes": [
{"text": "x ∈ s ∧ x ∈ t", "name": "h1", "id": "_uniq.99", "isProof": "proof"}
]
},
{
"tacticId": "6",
"hypNodes": [
{"text": "x ∈ t ∧ x ∈ s", "name": "h1", "id": "_uniq.116", "isProof": "proof"}
]
}
],
"hypTables": []
},
{
"id": "3",
"parentId": "1",
"goalNodes": [
{"text": "x ∈ t ∩ s → x ∈ s ∩ t", "name": "h.mpr", "id": "_uniq.65"},
{"text": "x ∈ s ∩ t", "name": "h.mpr", "id": "_uniq.125"}
],
"hypLayers": [
{
"tacticId": "8",
"hypNodes": [
{"text": "x ∈ t ∩ s", "name": "h2", "id": "_uniq.124", "isProof": "proof"}
]
},
{
"tacticId": "9",
"hypNodes": [
{"text": "x ∈ t ∧ x ∈ s", "name": "h2", "id": "_uniq.145", "isProof": "proof"}
]
},
{
"tacticId": "10",
"hypNodes": [
{"text": "x ∈ s ∧ x ∈ t", "name": "h2", "id": "_uniq.160", "isProof": "proof"}
]
}
],
"hypTables": []
}
],
"tactics": [
{
"id": "1",
"text": "init",
"dependsOnIds": [],
"goalArrows": [],
"hypArrows": [
{"shardId": "0", "fromId": null, "toIds": ["_uniq.30", "_uniq.31"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "2",
"text": "ext x",
"dependsOnIds": [],
"goalArrows": [
{"fromId": "_uniq.32", "toId": "_uniq.56"}
],
"hypArrows": [
{"shardId": "0", "fromId": null, "toIds": ["_uniq.55"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "3",
"text": "apply Iff.intro",
"dependsOnIds": [],
"goalArrows": [
{"fromId": "_uniq.56", "toId": "_uniq.64"},
{"fromId": "_uniq.56", "toId": "_uniq.65"}
],
"hypArrows": [],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "4",
"text": "intro h1",
"dependsOnIds": [],
"goalArrows": [
{"fromId": "_uniq.64", "toId": "_uniq.69"}
],
"hypArrows": [
{"shardId": "0", "fromId": null, "toIds": ["_uniq.68"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "5",
"text": "rw [Set.mem_inter_iff]",
"dependsOnIds": ["_uniq.68"],
"goalArrows": [],
"hypArrows": [
{"shardId": "0", "fromId": "_uniq.68", "toIds": ["_uniq.99"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "6",
"text": "rw [and_comm]",
"dependsOnIds": ["_uniq.99"],
"goalArrows": [],
"hypArrows": [
{"shardId": "0", "fromId": "_uniq.99", "toIds": ["_uniq.116"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "7",
"text": "exact h1",
"dependsOnIds": ["_uniq.116"],
"goalArrows": [],
"hypArrows": [],
"successGoalId": "_uniq.69",
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "8",
"text": "intro h2",
"dependsOnIds": [],
"goalArrows": [
{"fromId": "_uniq.65", "toId": "_uniq.125"}
],
"hypArrows": [
{"shardId": "0", "fromId": null, "toIds": ["_uniq.124"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "9",
"text": "rw [Set.mem_inter_iff]",
"dependsOnIds": ["_uniq.124"],
"goalArrows": [],
"hypArrows": [
{"shardId": "0", "fromId": "_uniq.124", "toIds": ["_uniq.145"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "10",
"text": "rw [and_comm]",
"dependsOnIds": ["_uniq.145"],
"goalArrows": [],
"hypArrows": [
{"shardId": "0", "fromId": "_uniq.145", "toIds": ["_uniq.160"]}
],
"haveBoxIds": [],
"byBoxIds": []
},
{
"id": "11",
"text": "exact h2",
"dependsOnIds": ["_uniq.160"],
"goalArrows": [],
"hypArrows": [],
"successGoalId": "_uniq.125",
"haveBoxIds": [],
"byBoxIds": []
}
],
"equivalentIds": {
"_uniq.69": ["_uniq.102", "_uniq.119"],
"_uniq.125": ["_uniq.148", "_uniq.163"]
}
}